TS
jhon702
Bank Soal Latihan Lengkap Persamaan Lingkaran
Bentuk-Bentuk Persamaan Lingkaran
• secara umum bentuk khusus persamaan lingkaran yang melewati titik pusat P(0,0) bentuk persamaannya menjadi x2 + y2 = r2 secara khusus persamaan lingkaran: (x-a)2 + (y-b)2 = r2
• persamaan lingkaran dengan pusat (a, b) dan berjari-jari r dapat dibentuk persamaan lingkaran menjadi (x-a)² + (y-b)² = r² .bentuk persamaan ini dinakaman bentuk khusus persamaan lingkaran
• hasil penjabaran dari (x-a)² + (y-b)² = r² akan membentuk bentuk umum persamaan lingkaran dapat dijabarkan menjadi:
(x-a)² + (y-b)² = r²
(x – a) (x – a) + (y – b) (y – b) = r²
x² – ax – ax + a² + y² – by – by + b²= r²
x² – 2ax + a² + y² – 2by - r² = 0
x² + y² – 2ax – 2by + a² + b² - r² = 0
maka dilakukan pemisalan dimana
A = -2a
B = -2b
c = a² + b² - r²
sehingga bentuk umum persamaan lingkaran:
x² + y² + Ax + By + C = 0.

1. persamaan lingkaran berpusat di (3, 5) dan menyinggung sumbu x adalah ..
e. i, ii, iii dan iv pernyataan benar
8. empat lingkaran berjari-jari satu satuan saling bersinggungan di sumbu koordinat (lihat gambar). dilukis lingkaran M yang berpusat di titik asal O dan menyinggung keempat lingkaran tadi. persamaan lingkaran M ialah .....
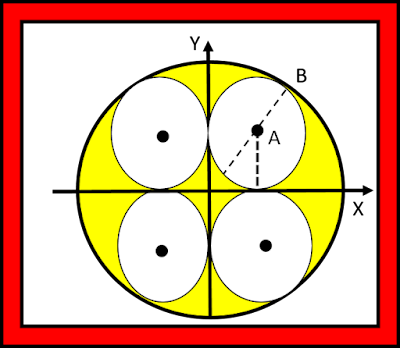
a. x² + y² = 4
Kunci Jawaban Serta Pembahasan Soal Lengkap____(Klik Disini)
• secara umum bentuk khusus persamaan lingkaran yang melewati titik pusat P(0,0) bentuk persamaannya menjadi x2 + y2 = r2 secara khusus persamaan lingkaran: (x-a)2 + (y-b)2 = r2
• persamaan lingkaran dengan pusat (a, b) dan berjari-jari r dapat dibentuk persamaan lingkaran menjadi (x-a)² + (y-b)² = r² .bentuk persamaan ini dinakaman bentuk khusus persamaan lingkaran
• hasil penjabaran dari (x-a)² + (y-b)² = r² akan membentuk bentuk umum persamaan lingkaran dapat dijabarkan menjadi:
(x-a)² + (y-b)² = r²
(x – a) (x – a) + (y – b) (y – b) = r²
x² – ax – ax + a² + y² – by – by + b²= r²
x² – 2ax + a² + y² – 2by - r² = 0
x² + y² – 2ax – 2by + a² + b² - r² = 0
maka dilakukan pemisalan dimana
A = -2a
B = -2b
c = a² + b² - r²
sehingga bentuk umum persamaan lingkaran:
x² + y² + Ax + By + C = 0.

1. persamaan lingkaran berpusat di (3, 5) dan menyinggung sumbu x adalah ..
a. x² + y² - 6x - 10y + 9 = 0
b. x² + y² + 6x + 10y + 9 = 0
c. x² + y² - 6x - 10y + 25 = 0
d. x² + y² + 6x + 10y + 25 = 0
e. x² + y² + 10x + 6y + 25 = 0
2. persamaan yang lingkaran berpusat di (-4, 2) dan menyinggung sumbu y adalah ..
a. x² + y² + 8x - 4y + 16 = 0
b. x² + y² - 8x + 4y + 16 = 0
c. x² + y² + 8x - 4y + 4 = 0
d. x² + y² + 8x + 4y + 4 = 0
e. x² + y² - 8x + 4y + 4 = 0
3. persamaan yang lingkaran berpusat di (2, 3) dan menyinggung garis y - 7 = 0 adalah ..
a. x² + y² - 4x - 6y + 7 = 0
b. x² + y² + 4x - 6y + 4 = 0
c. x² + y² + 4x + 6y + 4 = 0
d. x² + y² + 4x + 6y - 3 = 0
e. x² + y² - 4x - 6y - 3 = 0
4. persamaan lingkaran yang berpusat di (1, 2) dan menyinggung garis y = x adalah ..
a. x² + y² - 2x + 4y - 4$\frac {1}{2}$ = 0
b. x² + y² - 2x - 4y - 4$\frac {1}{2}$ = 0
c. x² + y² - 2x - 4y + 4$\frac {1}{2}$ = 0
d. x² + y² + 2x + 4y + 4$\frac {1}{2}$ = 0
e. x² + y² - 2x + 4y + 4$\frac {1}{2}$ = 0
5. lingkaran x² + y² - 2ax + 6y + 49 = 0 menyinggung sumbu X untuk a sama dengan ...
a. 7 dan -7
b. 2 dan -2
c. -6 dan 6
d. -3 dan 3
e. 5 dan -5
6. diketahui persamaan suatu lengkungan (x - p)² + (y - p)² = 25. supaya lengkungan ini menyinggung sumbu X, haruslah ..
a. p = 25
b. q = 25
c. q = 5 atau q = -5
d. p = 5 atau q = -5
e. p² + q² = 25
7. persamaan lingkaran yang menyinggung sumbu X dan sumbu Y dengan jari-jari 2 adalah ..
i). (x - 2)² + (y - 2)² = 4
ii).(x - 2)² + (y - 2)² = 4
iii).(x + 2)² + (y - 2)² = 4
iv).(x + 2)² + (y - 2)² = 4
a. i, ii dan iii pernyataan salah
b. i, ii dan iii pernyataan benar
c. i, ii dan iv pernyataan benar
d. i, ii dan iv pernyataan benar
e. i, ii, iii dan iv pernyataan benar
8. empat lingkaran berjari-jari satu satuan saling bersinggungan di sumbu koordinat (lihat gambar). dilukis lingkaran M yang berpusat di titik asal O dan menyinggung keempat lingkaran tadi. persamaan lingkaran M ialah .....

a. x² + y² = 4
b. x² + y² = 8
c. x² + y² = 3 + 2√2
d. x² + y² = 6 + 4√2
d. x² + y² = 9 + 4√2
9. pusat lingkaran 3x² + 3y² - 4x + 6y - 12 = 0 adalah ..
a. (2, 1)
b. (5, 9)
c. (2, 3)
d. (1/3, 5)
e. (2/3, -1)
10. sebuah titik A bergerak sedemikian sehingga jaraknya terhadap Q(0,0) senantiasa sama dengan dua kali jaraknya terhadap titik B(3, 0). tempat kedudukan titik A ini ialah lingkaran yang berpusat pada P dan mempunyai jari-jari r dengan ..
a. P(4,0) dan r = 4
b. P(4, 0) dan r = 2
c. P(0, 4) dan r = 2
d. P(0, 4) dan r = 4
e. P(-4, 0) dan r = 4
11. persamaan lingkaran berpusat di titik (2, 3) yang melalui (5, -1) adalah ...
a. x² + y² - 4x - 6y - 12 = 0
b. x² + y² - 4x - 6y - 25 = 0
c. x² + y² - 4x - 6y - 13 = 0
d. x² + y² - 2x - 3y - 10 = 0
e. x² + y² + 2x + 3y + 25 = 0
12. diketahui titik A(-2, 1) dan B(4, -3) jika titik P(x, y) terletak sedemikian sehingga (PA)² + (PB)² = (AB)², maka P merupakan titik-titik yang terletak pada busur lingkaran yang memotong sumbu X adalah ..
a. x = 2√3 + 1 dan x = 2√3 - 1
b. x = 2√3 + 1 dan x = -2√3 + 1
c. x = 2√3 - 1 dan x = -2√3 - 1
d. x = 2√3 - 1 dan x = -2√3 - 1
e. x = -2√3 - 1 dan x = -2√3 - 1
13. persamaan garis singgung di titik (-3, 4) pada lingkaran x² + y² = 25 adalah ...
a. y = $\frac {4x}{3}$ - $\frac {25}{3}$
b. y = $\frac {-4x}{3}$ + $\frac {25}{3}$
c. y = $\frac {-3x}{4}$ + $\frac {25}{4}$
d. y = $\frac {3x}{4}$ - $\frac {25}{4}$
e. y = $\frac {3x}{4}$ + $\frac {25}{4}$
14. persamaan garis singgung melalui titik (5, 1) pada lingkaran x² + y² - 4x + 6y - 12 = 0 adalah ...
a. 3x + 4y - 19 = 0
b. 3x - 4y - 19 = 0
c. 4x - 3y + 19 = 0
d. x + 7y - 26 = 0
e. x - 7y - 26 = 0
15. persamaan garis singgung lingkaran x² + y² = 25 yang dapat ditarik dari (7, 1) adalah ...
a. x - 2y = 25 dan x + 3y = 25
b. 4x - 3y = 25 dan 3x + 4y = 25
c. 2x - 4y = 25 dan 2x + 4y = 25
d. 7x + y = 25 dan 7x - y = 25
e. 7x + y = 25 dan 7x + 3y = 25
16. garis yang melalui (0, 2) dan menyinggung kurva x² + y² = 25 adalah:
a. y = -x + 2
b. y = x + 1
c. y = x - 2
d. y = x - 1
e. tidak ada
17. lingkaran x² + y² - 2px + q = 0 yang mempunyai jari-jari 2 akan menyinggung garis x - y = 0. bila nilai p yang positif sama dengan...
a. 2
b. 2√2
c. 4
d. 4√2
e. 8
18. jika titik (-5, k) terletak pada lingkaran x² + y² + 2x - 5y - 21 = 0, maka nilai k adalah ..
a. -1 atau -2
b. 2 atau 4
c. -1 atau 6
d. 0 atau 3
e. 1 atau -6
19. jarak terdekat antara titik (-7, 2) ke lingkaran x² + y² - 10x - 14y - 151 = 0 sama dengan ..
a. 2
b. 4
c. 3
d. 8
e. 13
20. persamaan garis lurus yang melalui pusat lingkaran x² + y² - 2x - 4y + 2 = 0 dan tegak lurus garis 2x - y + 3 = 0 adalah ...
a. x + 2y - 3 = 0
b. 2x + y + 1 = 0
c. x + 2y - 5 = 0
d. x - 2y -1 = 0
e. 2x - y - 1 = 0
21. dua buah lingkaran dengan persamaan-persamaan x² + y² + 6x - 8y + 21 = 0 dan x² + y² + 10x - 8y + 25 = 0 kedua lingkaran ini ...
a. berpotongan di dua titik
b. tidak berpotongan atau bersinggungan
c. bersinggungan di luar
d. bersinggungan di dalam
e. sepusat
22. persamaan tali busur persekutuan (x - 3)² + y² = 16 dan x² + (y - 3)² = 16 adalah ...
a. y = -2x
b. y = -x
c. y = x
d. y = 2x
e. y = $\frac {1}{2}$
23. lingkaran berpusat di titik asal O dan berjari-jari 3 memotong sumbu X positif, sumbu Y positif, dan sumbu Y negatif berturut-turut di titik A, B, dan C. dibuat garis singgung di B. garis melalui CA memotong garis singgung tersebut di titik P. koordinat P ialah...
a. (3, 6)
b. (3$\frac {1}{3}$, 6)
c. (6, 3(1/3)
d. (6, 3)
e. (6, 6)
Kunci Jawaban Serta Pembahasan Soal Lengkap____(Klik Disini)
Diubah oleh jhon702 05-07-2022 12:13
0
642
0
Komentar yang asik ya
Komentar yang asik ya
Komunitas Pilihan