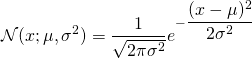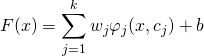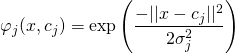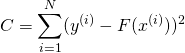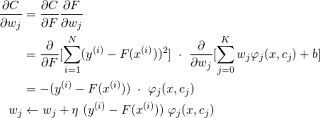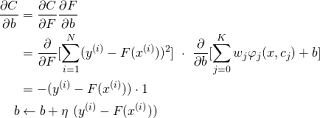RBF net dapat digunakan untuk aproksimasi sebuah model forecasting yang mempresentasikan sebuah data yang mengandung pola trend.  RBF menggunakan distribusi gaussian sebagai basis function nya.  Sebelum melangkah lebih jauh mengenai RBF, maka perlu sedikit membahas distribusi gaussian. 

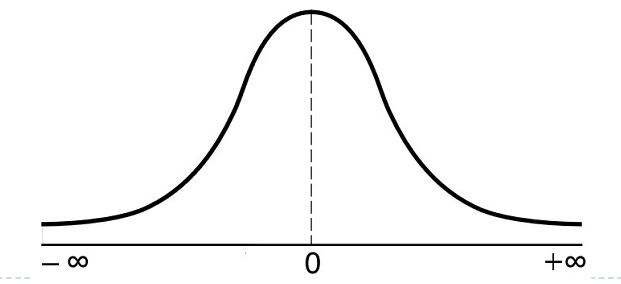
Distribusi  ini  memiliki  parameter  berupa  mean  (µ) dan simpangan baku  (σ). Distribusi normal  dengan  µ=0  dan        σ  =1  disebut dengan  distribusi  normal  standar.    Apabila digambarkan  dalam  grafk,  kurva  nya  akan berbentuk seperti lonceng

Sumbu  horizontal  memiliki  rentang  negatif  tak hingga sampai  positif tak hingga. Secara  matematis,    probabilitas  distribusi normal  standar  kumulatif  dapat  dihitung dengan  menggunakan  rumus  sebagai berikut :

µ disebut dengan mean/rerata
σ disebut standar deviasi
σ2 disebut variance

Untuk menentukan sebuah centroid data, kita bisa menggunakan K-Means clustering dengan cj sebagai centroid data untuk setiap radial basis function ҩj ,maka untuk setiap data x pada setiap RBF akan menghasilkan sebuah bobot dan bias dengan persamaan berikut:

wj adalah bobot
bi adalah bias
ki adalah jumlah cluster
ҩj adalah radial basis function dari Gaussian dengan detail sebagai berikut

Dari definisi diatas, maka kita dapat menghitung turun dari wj dan bi dengan teknik gradien descent (quadratic cost function to minimize)

Turunan fungsi terhadap wj

Turunan fungsi terhadap bi

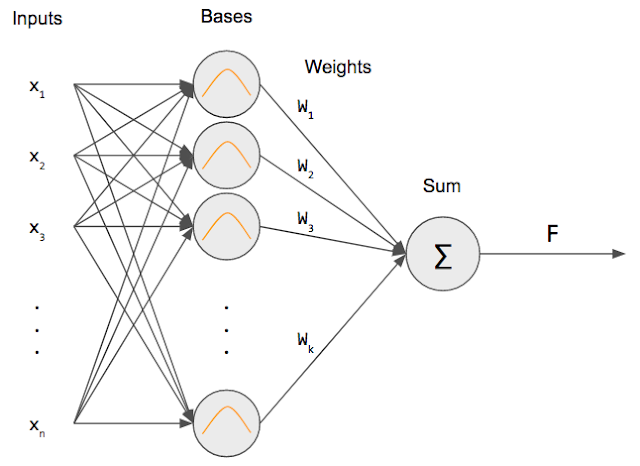
Sehingga model RBF Net seperti berikut

Code ditulis menggunakan Python, dengan beberapa library seperti Numpy, Matplotlib, serta Sklearn, silahkan pelajari Python di http://www.softscients.web.id/2018/1...n-dengan.html.
Kita akan membuat 2 fungsi utama yaitu rbf()dan kmeans()

def rbf(x, c, s):

    '''

    c adalah mean yang berasal dari centroid kmeans

    s adalah standar deviasi masing-masing anggota kmeans

    '''

    

    return np.exp(-1 / (2 * s**2) * (x-c)**2)

Khusus untuk Kmeans, kita gunakan pustaka Sklearn saja, dengan sedikit modifikasi yaitu dengan menambahkan sedikit code untuk menghitung standar deviasi untuk masing-masing anggota kelas.

def kmeans2(X,k):

    '''

 ref:https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html

    '''

    p = np.reshape(X,[len(X),1])

    k_means = KMeans(n_clusters=k,init='random',n_init=30)

    k_means.fit(p)

    stds = list()

    for i in range(0,k):

        stds.append(np.std(y[k_means.labels_==i])) #hitung std

    stds = np.array(stds)

    center  = k_means.cluster_centers_

    center = np.reshape(center,[len(center)]) #ubah dimensi

    return center, stds

Class RBF untuk neural networknya

class RBFNet(object):

    """Implementation of a Radial Basis Function Network"""

    def __init__(self, k=2, lr=0.01, epochs=100, rbf=rbf):

        self.k = k

        self.lr = lr

        self.epochs = epochs

        self.rbf = rbf

        



        self.w = np.random.randn(k)

        self.b = np.random.randn(1)



    def fit(self, X, y):        

        # compute stds from data        

        self.centers, self.stds = kmeans2(X, self.k)



        # training

        for epoch in range(self.epochs):

            for i in range(X.shape[0]):

                # forward pass

                a = np.array([self.rbf(X[i], c, s) for c, s, in zip(self.centers, self.stds)])

                F = a.T.dot(self.w) + self.b



                loss = (y[i] - F).flatten() ** 2

                print('Loss: {0:.2f}'.format(loss[0]))



                # backward pass

                error = -(y[i] - F).flatten()



                # online update

                self.w = self.w - self.lr * a * error

                self.b = self.b - self.lr * error



    def predict(self, X):

        y_pred = []

        for i in range(X.shape[0]):

            a = np.array([self.rbf(X[i], c, s) for c, s, in zip(self.centers, self.stds)])

            F = a.T.dot(self.w) + self.b

            y_pred.append(F)

        return np.array(y_pred)

Kode selengkapnya kunjungi saja: www.softscients.web.id
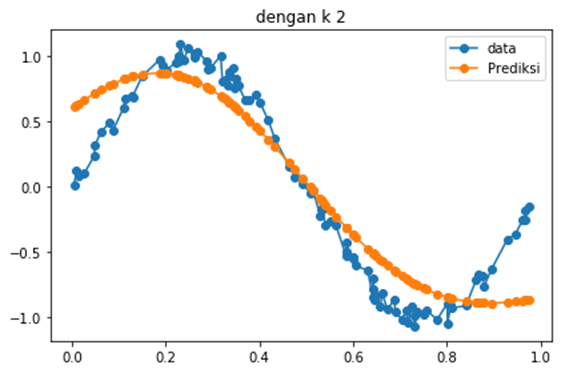
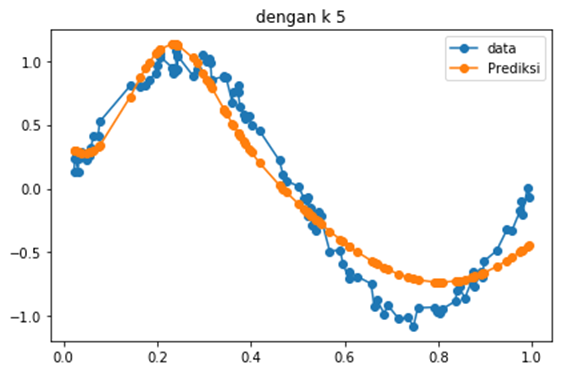
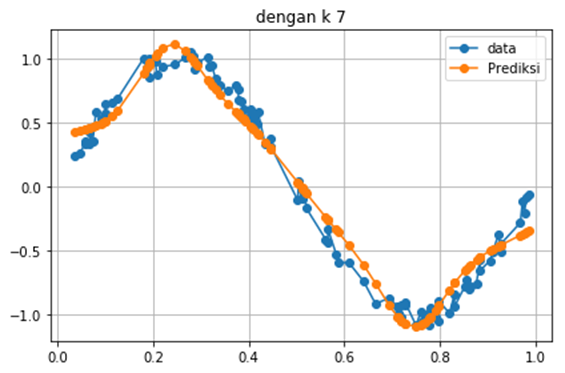
Mari kita coba untuk membuat forecasting sebuah data yang mengandung sebuah tren berikut

Dengan nilai K semakin besar, maka data prediksi semakin smooth
Ref:
https://scikit-learn.org/stable/modu...er.KMeans.html
https://en.wikipedia.org/wiki/Radial...basis_function
https://miqbal.staff.telkomuniversit...is-distribusi/