- Beranda
- Komunitas
- News
- Sains & Teknologi
P vs. NP, masalah yang berhadiah US$ 1.000.000
TS
Qidran
P vs. NP, masalah yang berhadiah US$ 1.000.000
Udah dicek gan, no repost 

Quote:
Pendahuluan
Quote:
Di tahun 2000, Institut Matematik Clay memberikan sayembara berupa penyelesaian untuk tujuh masalah yang kronis dalam matematik, yang disebut ‘Millenium Prize Problem.’ Orang yang berhasil menyelesaikan salah satu dari permasalahan ini berhak atas uang US$ 1.000.000. Ada tujuh permasalahan:

Dan ya, ada satu yang berhasil menyelesaikannya, tapi yang jelas bukan P vs. NP. Dia menolak tawaran hadiah, tapi kalo kita bisa kita bakal nolak?
Gak segampang itu bro, untuk memahami dari problem-problem yang disayembarain itu butuh pemahaman tinggi, bahkan harus bergelar PhD, DEA, apalah itu, karena memang masalah-masalah ini sangat kompleks dan sulit untuk dipecahkan bahkan untuk orang awam. Jadi kalo memang mau memahami dan menyelesaikan masalah ini, silahkan belajar yang tekun dan rajin (Y).
Di antara semuanya, P vs. NP adalah masalah yang paling mudah buat dipahami, tapi sama-sama sulit untuk dipecahkan. Sekali lagi, kalo memang mau dapet hadiah US$ 1.000.000 silahkan pahami trit ini, dan rumusin sama agan sendiri penyelesaiannya, tentu matematis ya. Tapi kalo buat sekedar ilmu, ya boleh kali ye cendol sama rate limanya nanti.
Quote:

1. Dugaan Poincare
2. P vs. NP
3. Dugaan Hodge
4. Hipotesis Riemann
5. Teori Yang-Mills
6. Persamaan Navier-Stokes untuk fluida ‘Smooth’
7. Dugaan Birch dan Swinnerton-Dyer
2. P vs. NP
3. Dugaan Hodge
4. Hipotesis Riemann
5. Teori Yang-Mills
6. Persamaan Navier-Stokes untuk fluida ‘Smooth’
7. Dugaan Birch dan Swinnerton-Dyer
Dan ya, ada satu yang berhasil menyelesaikannya, tapi yang jelas bukan P vs. NP. Dia menolak tawaran hadiah, tapi kalo kita bisa kita bakal nolak?
Gak segampang itu bro, untuk memahami dari problem-problem yang disayembarain itu butuh pemahaman tinggi, bahkan harus bergelar PhD, DEA, apalah itu, karena memang masalah-masalah ini sangat kompleks dan sulit untuk dipecahkan bahkan untuk orang awam. Jadi kalo memang mau memahami dan menyelesaikan masalah ini, silahkan belajar yang tekun dan rajin (Y).
Di antara semuanya, P vs. NP adalah masalah yang paling mudah buat dipahami, tapi sama-sama sulit untuk dipecahkan. Sekali lagi, kalo memang mau dapet hadiah US$ 1.000.000 silahkan pahami trit ini, dan rumusin sama agan sendiri penyelesaiannya, tentu matematis ya. Tapi kalo buat sekedar ilmu, ya boleh kali ye cendol sama rate limanya nanti.
Quote:
Kompleksivitas?
Quote:
Bertahun lalu, ketika awal adanya komputer, orang-orang mulai membuat mesin yang simpelnya bisa berhitung. Mikirnya begini, kalo komputer bisa lebih cepat kenapa gak pake komputer aja? Jadi dipakai komputer buat menghitung persamaan-persamaan differensiasi, integral, transformasi, diskrit, dan lainnya. Tapi dulu komputer buat ngitung kayak gituan butuh waktu lama buat mencari jawabannya, dan seiring waktu ternyata komputer yang semakin berkembang malah mempercepat proses perhitungan.
Komputer kalau diberi tugas perkalian, pengurangan, penambahan, pembagian, dan pengurutan deret ternyata akan semakin cepat dengan semakin bagusnya komputer.
Tapi nyatanya, ada beberapa problem yang gak bisa berjalan cepat untuk cari jawabannya. Salah satu contohnya adalah masalah ‘salesman keliling.’
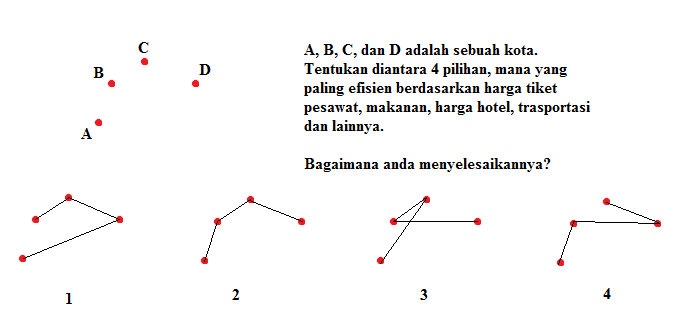
Bagaimana cara anda menyelesaikannya? Satu-satunya cara adalah melalui mencarinya melalui berbagai jawaban yang mungkin bisa dihasilkan. Asumsi di atas adalah apabila kegiatan penjualan dimulai dari Kota A, namun bagaimana jika dimulai dari Kota B, C, atau D? Yah, bahkan komputer sekalipun akan sangat kewalahan untuk mencari jalan yang paling murah untuk berjualan.
Masalah ini sering disebut sebagai optimatisasi untuk mencari biaya termurah dan optimal untuk para sales. Masalah ini tidak bisa diselesaikan dengan cepat, karena terlalu banyak faktor yang mempengaruhi seperti tiket pesawat, biaya makan, biaya hotel, dan lain-lain.
Disini dimana orang-orang mulai mengelompokkan berbagai permasalahan, mana yang cepat diselesaikan,dan mana yang memang lama untuk diselesaikan oleh komputer. Dan orang-orang juga mengelompokkan beberapa yang mungkin dan bisa jadi susah atau mudah.
Jadi orang masih terus berusaha, apa memang ada program yang lebih baik dan komputer berperforma tinggi yang dapat menyelesaikan masalah-masalah yang belum terklasifikasi antara cepat dan lambat.
Disinilah munculnya P dan NP.
P adalah apa yang disebut sebagai Polynomial Time (Waktu Polinomial). Artinya jumlah tahapan penyelesaian ada dalam bentuk persamaan polinomial besar masalahnya.
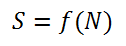
S adalah jumlah tahapan penyelesaian, dan N adalah besar masalahnya. f(N) adalah bentuk persamaan polinomial. Persamaan polinomial adalah seperti berikut:
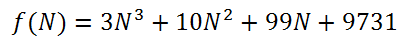
Tapi bukan seperti berikut:
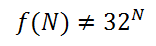
Maksudnya adalah, jumlah tahapan penyelesaian tidak begitu banyak dan luar biasa banyaknya jika dibandingkan dengan besarnya masalah, seperti penambahan, 1+1, tidak akan berbeda dengan 1+3240, ya kan? Sama-sama hanya satu kali jalan, tanpa merubah jumlah tahapan penyelesaian dan tidak menambah jauh waktu untuk penyelesaian.
Sedangkan NP adalah Non-Deterministic Polynomial Time (Waktu Polinomial Non-Deterministik). Ini adalah bentuk non deterministik dari P, dimana kita akan mencari seberapa banyak kemungkinan jawaban yang benar dari waktu polinomial. Tentu ini akan memakan banyak waktu karena jawabannya tidaklah deterministik dan memiliki banyak kemungkinan. Ini layaknya masalah mencari jawaban ‘trial dan error’ ketika memecahkan masalah faktorisasi persamaan kuadrat atau mungkin... Sudoku?
Jadi ya, melihat beberapa sumber, memang lebih enak menjelaskannya dari puzzle seperti sudoku.
Komputer kalau diberi tugas perkalian, pengurangan, penambahan, pembagian, dan pengurutan deret ternyata akan semakin cepat dengan semakin bagusnya komputer.
Tapi nyatanya, ada beberapa problem yang gak bisa berjalan cepat untuk cari jawabannya. Salah satu contohnya adalah masalah ‘salesman keliling.’
Spoiler for Travelling Salesman Problem:

Bagaimana cara anda menyelesaikannya? Satu-satunya cara adalah melalui mencarinya melalui berbagai jawaban yang mungkin bisa dihasilkan. Asumsi di atas adalah apabila kegiatan penjualan dimulai dari Kota A, namun bagaimana jika dimulai dari Kota B, C, atau D? Yah, bahkan komputer sekalipun akan sangat kewalahan untuk mencari jalan yang paling murah untuk berjualan.
Masalah ini sering disebut sebagai optimatisasi untuk mencari biaya termurah dan optimal untuk para sales. Masalah ini tidak bisa diselesaikan dengan cepat, karena terlalu banyak faktor yang mempengaruhi seperti tiket pesawat, biaya makan, biaya hotel, dan lain-lain.
Disini dimana orang-orang mulai mengelompokkan berbagai permasalahan, mana yang cepat diselesaikan,dan mana yang memang lama untuk diselesaikan oleh komputer. Dan orang-orang juga mengelompokkan beberapa yang mungkin dan bisa jadi susah atau mudah.
Jadi orang masih terus berusaha, apa memang ada program yang lebih baik dan komputer berperforma tinggi yang dapat menyelesaikan masalah-masalah yang belum terklasifikasi antara cepat dan lambat.
Spoiler for Permasalahan:

Disinilah munculnya P dan NP.
P adalah apa yang disebut sebagai Polynomial Time (Waktu Polinomial). Artinya jumlah tahapan penyelesaian ada dalam bentuk persamaan polinomial besar masalahnya.
Quote:
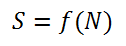
S adalah jumlah tahapan penyelesaian, dan N adalah besar masalahnya. f(N) adalah bentuk persamaan polinomial. Persamaan polinomial adalah seperti berikut:
Quote:
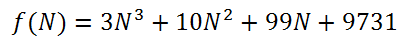
Tapi bukan seperti berikut:
Quote:
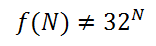
Maksudnya adalah, jumlah tahapan penyelesaian tidak begitu banyak dan luar biasa banyaknya jika dibandingkan dengan besarnya masalah, seperti penambahan, 1+1, tidak akan berbeda dengan 1+3240, ya kan? Sama-sama hanya satu kali jalan, tanpa merubah jumlah tahapan penyelesaian dan tidak menambah jauh waktu untuk penyelesaian.
Sedangkan NP adalah Non-Deterministic Polynomial Time (Waktu Polinomial Non-Deterministik). Ini adalah bentuk non deterministik dari P, dimana kita akan mencari seberapa banyak kemungkinan jawaban yang benar dari waktu polinomial. Tentu ini akan memakan banyak waktu karena jawabannya tidaklah deterministik dan memiliki banyak kemungkinan. Ini layaknya masalah mencari jawaban ‘trial dan error’ ketika memecahkan masalah faktorisasi persamaan kuadrat atau mungkin... Sudoku?
Jadi ya, melihat beberapa sumber, memang lebih enak menjelaskannya dari puzzle seperti sudoku.
Quote:
Sudoku??
Quote:
Sebelumnya lihat diagram dulu untuk mengingatkan.
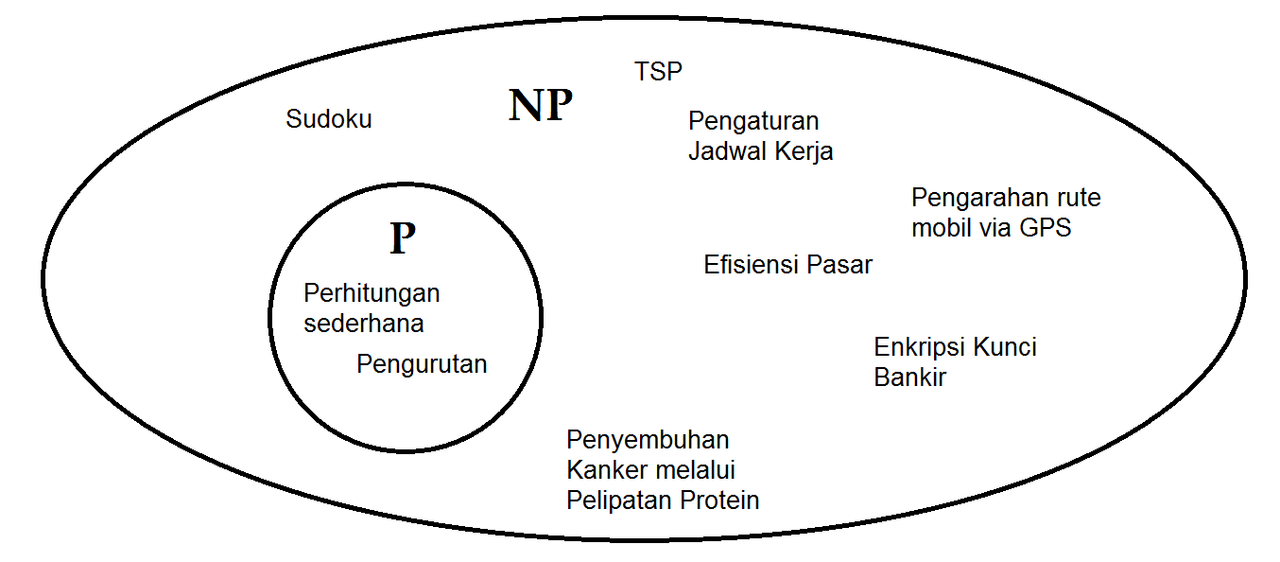
P adalah kelompok masalah yang mudah, seperti perhitungan aritmatik sederhana, tambah, kurang, bagi, kali, dan pengurutan. P adalah masalah yang dimana jawabannya jika kita ingin mengetahuinya, kita tinggal melalui prosesnya saja.
Jika kalau ada bocoran 2.000.000 dikali 10 sama dengan 20.000.000, bagaimana agan bisa tahu kalau bocoran itu benar? Ya gampang, kita tinggal kaliin aja sendiri, iya gak? Pake coret-coretan biasa juga kita bisa.
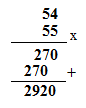
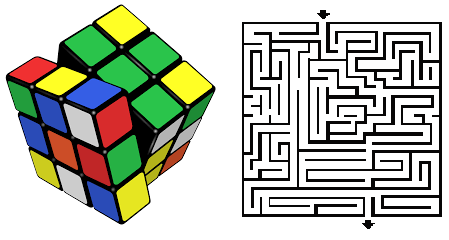
Permasalahan P juga termasuk Rubik dan Labirin. Contohnya kita tahu Rubik itu tiap sisi punya warna sama, nah bagaimana kita bisa membuat Rubik yang tadinya acak jadi sisinya sama semua warnanya? Ya kita tinggal di balikin seperti semula melalui prosesnya memutar-membalik. Kalau di Labirin kita tahu dimana pintu masuk dan pintu keluar, dan untuk mengetahui, kita tinggal menggaris jalannya saja, itu adalah prosesnya.
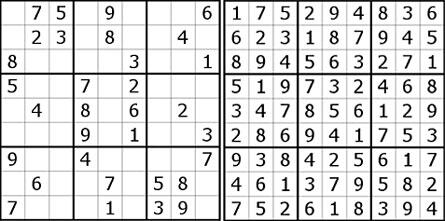
Sedangkan NP adalah kelompok masalah yang dibilang agak susah, seperti Sudoku. Memang sulit menyelesaikan Sudoku, tapi kalau kita mengetahui kunci jawabannya, kita mudah mengecek jawabannya dan mengecek mana yang salah dan benar tinggal hapus dan ganti.

Jangan salah, Tetris dan Battleship adalah game serupa dengan inti permasalahan yang sama dengan problem TSP
Tapi masalahnya adalah jika kita belum tahu kunci jawabannya, sedangkan untuk mengetahui itu benar atau tidak, butuh kunci jawaban untuk mengecek jawaban kita. Jadi artinya penyelesaian Sudoku jauh lebih lama daripada mengecek apakah jawaban itu benar atau tidak. Kesimpulan yang bagus, tapi tidak juga. Itu belum tentu juga.
Orang mulai berpikir, Kalau kita bisa mengecek jawaban benar saja cepat, bagaimana dengan mencari jawaban benar dengan cepat?
Sehingga muncul pertanyaan P vs. NP
Ya, itu dia pertanyaan seharga US$ 1.000.000. Yang menyelesaikannya dengan hormat akan dapat kesempatan yang berharga untuk berfoya-foya.
Tapi tunggu dulu ini hanya permulaan dari kompleksivitas!
Coba buat di kalkulator 987654321 x 123456789 dan terus pencet ‘=’. Pasti delaynya sangat kecil kan? Tentu, ini namanya masalah P. Kalkulator cepat mengetahui jawabannya benar karena kalkulator cepat mencari jawaban benarnya.
Tapi serasa bagi kita kalau kita hitung sendiri pake coretan sederhana, rasanya mustahil. Ini namanya sulit untuk manusia tapi mudah untuk komputer. Sama seperti Rubik atau Labirin.
Bagaimana dengan Sudoku?
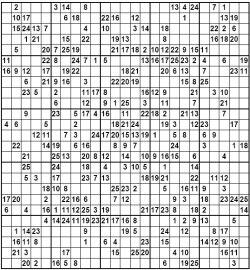
Sudoku akan terlihat mudah di mata komputer kalau ukurannya tidak terlalu besar. Ukuran normal 9x9 pasti akan selesai dalam beberapa milisekon, tapi kalau sudah 100.000x100.000? Komputer super pun akan kelabakan!
Quote:

P adalah kelompok masalah yang mudah, seperti perhitungan aritmatik sederhana, tambah, kurang, bagi, kali, dan pengurutan. P adalah masalah yang dimana jawabannya jika kita ingin mengetahuinya, kita tinggal melalui prosesnya saja.
Jika kalau ada bocoran 2.000.000 dikali 10 sama dengan 20.000.000, bagaimana agan bisa tahu kalau bocoran itu benar? Ya gampang, kita tinggal kaliin aja sendiri, iya gak? Pake coret-coretan biasa juga kita bisa.
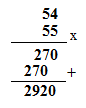
Permasalahan P juga termasuk Rubik dan Labirin. Contohnya kita tahu Rubik itu tiap sisi punya warna sama, nah bagaimana kita bisa membuat Rubik yang tadinya acak jadi sisinya sama semua warnanya? Ya kita tinggal di balikin seperti semula melalui prosesnya memutar-membalik. Kalau di Labirin kita tahu dimana pintu masuk dan pintu keluar, dan untuk mengetahui, kita tinggal menggaris jalannya saja, itu adalah prosesnya.
Spoiler for Permasalahan P:

Sedangkan NP adalah kelompok masalah yang dibilang agak susah, seperti Sudoku. Memang sulit menyelesaikan Sudoku, tapi kalau kita mengetahui kunci jawabannya, kita mudah mengecek jawabannya dan mengecek mana yang salah dan benar tinggal hapus dan ganti.
Spoiler for Permasalahan NP:

Jangan salah, Tetris dan Battleship adalah game serupa dengan inti permasalahan yang sama dengan problem TSP
Tapi masalahnya adalah jika kita belum tahu kunci jawabannya, sedangkan untuk mengetahui itu benar atau tidak, butuh kunci jawaban untuk mengecek jawaban kita. Jadi artinya penyelesaian Sudoku jauh lebih lama daripada mengecek apakah jawaban itu benar atau tidak. Kesimpulan yang bagus, tapi tidak juga. Itu belum tentu juga.

Orang mulai berpikir, Kalau kita bisa mengecek jawaban benar saja cepat, bagaimana dengan mencari jawaban benar dengan cepat?
Sehingga muncul pertanyaan P vs. NP
Spoiler for Pertanyaan 1 Juta Dollar:
“Jika kita bisa mengenali jawaban yang benar dengan cepat, apa kita bisa dengan cepat mencarinya?”
Ya, itu dia pertanyaan seharga US$ 1.000.000. Yang menyelesaikannya dengan hormat akan dapat kesempatan yang berharga untuk berfoya-foya.
Tapi tunggu dulu ini hanya permulaan dari kompleksivitas!
Coba buat di kalkulator 987654321 x 123456789 dan terus pencet ‘=’. Pasti delaynya sangat kecil kan? Tentu, ini namanya masalah P. Kalkulator cepat mengetahui jawabannya benar karena kalkulator cepat mencari jawaban benarnya.
Tapi serasa bagi kita kalau kita hitung sendiri pake coretan sederhana, rasanya mustahil. Ini namanya sulit untuk manusia tapi mudah untuk komputer. Sama seperti Rubik atau Labirin.
Bagaimana dengan Sudoku?

Sudoku akan terlihat mudah di mata komputer kalau ukurannya tidak terlalu besar. Ukuran normal 9x9 pasti akan selesai dalam beberapa milisekon, tapi kalau sudah 100.000x100.000? Komputer super pun akan kelabakan!
Quote:
Hirarki
Quote:
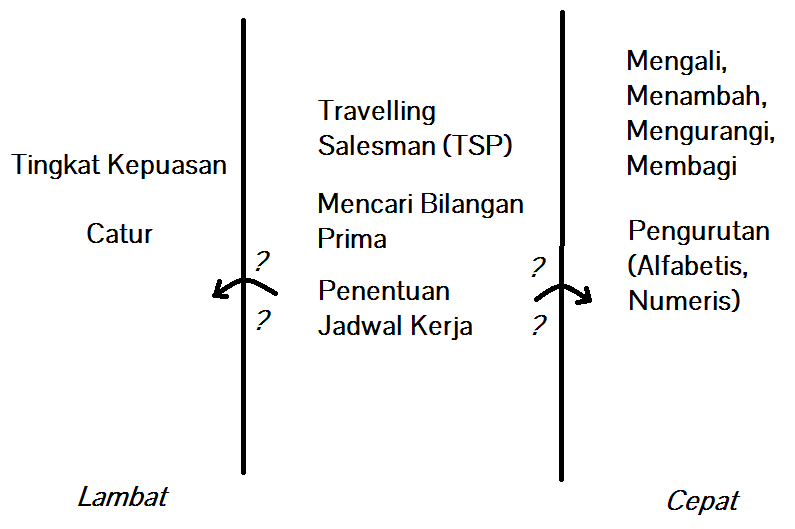
Sepertinya P dan NP hanyalah sebuah daya tarik yang mendasar dari berbagai macam hirarki kesulitan kompleksivitas dalam komputasi. P dan NP hanya memberi sebagian kecil dari apa yang akan menjadi sebuah ‘Kebun Kompleksivitas’.
P dan NP adalah sebuah permulaan.
P dan NP rupanya hanya sebagian kecil dari kebun kompleksivitas. Di NP, terdapat sebuah kelompok yang disebut sebagai NP-Komplit. Bisa dibilang NP-komplit adalah bagian tersulit dari NP. Di dalam NP-komplit ada yang disebut dengan NP-sulit atau NP-hard. Istilah ini merujuk pada problem-problem dengan tingkat kesulitan NP yang sangat tinggi. Beberapa diantaranya adalah masalah kepuasan, pencocokan 3-dimensi, hingga pengaturan jadwal kerja.
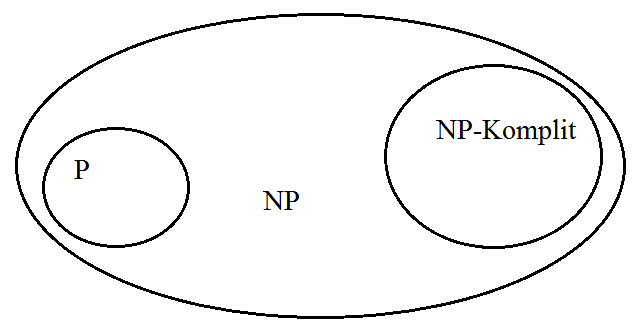
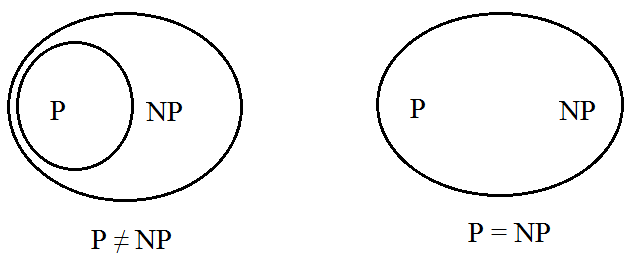
Apabila agan bisa menemukan sebuah mesin yang bisa menyelesaikan masalah setidaknya salah satu yang disebutkan dengan cepat, maka mesin itu bisa menyelesaikan seluruh permasalahan dalam NP, sehingga seluruh sistem NP kolaps menjadi P, maka P=NP! Namun apabila memang tidak ada mesin yang cepat untuk masalah NP-sulit, maka P≠NP. Jadi ya sampai sekarang masih belum ada yang tahu, semua orang masih mencoba.
Tak berhenti disitu, di dalam P, masih ada kelompok NL atau Non-deterministic Logarithmic Space (Ruang Logarithmik Non-deterministik) dan di dalamnya ada L atau Logarithmic Space (Ruang Logaritmik). Dan di dalam L masih ada AC atau Alternating Class.
Diluar NP ada EXP atau Exponential Polinomial. Disini adalah tempat dimana puzzle jadi kurang bermutu, seperti apa langkah terbaik untuk memenangkan Catur?
Jawabannya adalah tidak tahu. Karena siapa yang tahu, untuk melakukan satu kali gerakan saja bisa dibalas untuk ribuan kemungkinan yang bisa terjadi. Komputer pun akan kesakitan untuk memikirkannya karena perhitungannya terlalu besar dan luas!
Disamping NP ada yang namanya Co-NP. Co-NP adalah kelompok masalah yang berhubungan dengan Tautologi atau sebuah pernyataan yang menyatakan kalimat betul untuk semua premis yang terjadi dalam suatu peristiwa.
Di dalam EXP namun diluar NP ada sebuah kelompok masalah yang disebut PSPACE atau Polinomial Space dimana salah satu masalah yang menyangkut ruang dalam polinomial seperti permainan dibawah.
Apa langkah terbaik untuk menyelesaikan permainan diatas?
Di dalam PSPACE masih ada BPP dan BQP dan di luar dari EXP masih ada hirarki yang lebih besar lagi, seperti EXPSPACE dan diatasnya masih ada lagi 2-EXP dan terus hingga kelompok tertinggi ke masalah penentuan (Decideable) dan hingga ke masalah pelimitan.
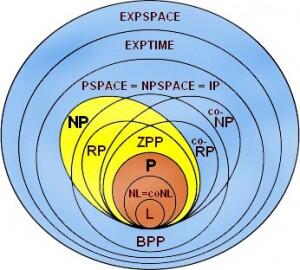
Memang ternyata kompleksivitas masih rumit dari yang dipikirkan. Masih ada pertanyaan seperti NP vs. Co-NP, L vs. NL, dan sebagainya. Sepertinya untuk NP dan P adalah fokus utama untuk para ilmuwan kompleksivitas saat ini.
P dan NP adalah sebuah permulaan.
P dan NP rupanya hanya sebagian kecil dari kebun kompleksivitas. Di NP, terdapat sebuah kelompok yang disebut sebagai NP-Komplit. Bisa dibilang NP-komplit adalah bagian tersulit dari NP. Di dalam NP-komplit ada yang disebut dengan NP-sulit atau NP-hard. Istilah ini merujuk pada problem-problem dengan tingkat kesulitan NP yang sangat tinggi. Beberapa diantaranya adalah masalah kepuasan, pencocokan 3-dimensi, hingga pengaturan jadwal kerja.
Quote:

Apabila agan bisa menemukan sebuah mesin yang bisa menyelesaikan masalah setidaknya salah satu yang disebutkan dengan cepat, maka mesin itu bisa menyelesaikan seluruh permasalahan dalam NP, sehingga seluruh sistem NP kolaps menjadi P, maka P=NP! Namun apabila memang tidak ada mesin yang cepat untuk masalah NP-sulit, maka P≠NP. Jadi ya sampai sekarang masih belum ada yang tahu, semua orang masih mencoba.
Quote:

Tak berhenti disitu, di dalam P, masih ada kelompok NL atau Non-deterministic Logarithmic Space (Ruang Logarithmik Non-deterministik) dan di dalamnya ada L atau Logarithmic Space (Ruang Logaritmik). Dan di dalam L masih ada AC atau Alternating Class.
Diluar NP ada EXP atau Exponential Polinomial. Disini adalah tempat dimana puzzle jadi kurang bermutu, seperti apa langkah terbaik untuk memenangkan Catur?
Quote:

Jawabannya adalah tidak tahu. Karena siapa yang tahu, untuk melakukan satu kali gerakan saja bisa dibalas untuk ribuan kemungkinan yang bisa terjadi. Komputer pun akan kesakitan untuk memikirkannya karena perhitungannya terlalu besar dan luas!
Disamping NP ada yang namanya Co-NP. Co-NP adalah kelompok masalah yang berhubungan dengan Tautologi atau sebuah pernyataan yang menyatakan kalimat betul untuk semua premis yang terjadi dalam suatu peristiwa.
Di dalam EXP namun diluar NP ada sebuah kelompok masalah yang disebut PSPACE atau Polinomial Space dimana salah satu masalah yang menyangkut ruang dalam polinomial seperti permainan dibawah.
Spoiler for Game:

Apa langkah terbaik untuk menyelesaikan permainan diatas?
Di dalam PSPACE masih ada BPP dan BQP dan di luar dari EXP masih ada hirarki yang lebih besar lagi, seperti EXPSPACE dan diatasnya masih ada lagi 2-EXP dan terus hingga kelompok tertinggi ke masalah penentuan (Decideable) dan hingga ke masalah pelimitan.
Quote:

Memang ternyata kompleksivitas masih rumit dari yang dipikirkan. Masih ada pertanyaan seperti NP vs. Co-NP, L vs. NL, dan sebagainya. Sepertinya untuk NP dan P adalah fokus utama untuk para ilmuwan kompleksivitas saat ini.
Quote:
Penutup
Quote:
Jadi apa sih akibatnya untuk masalah P vs. NP ini buat kita?
Ada beberapa masalah yang perlu kita ketahui dengan cepat namun masalahnya berbasis NP. Seperti optimalisasi pasar, optimalisasi tingkat kepuasan, menentukan jadwal bekerja yang optimal dengan maksimal, menentukan rute jalan terbaik dengan cepat dan bahkan pelipatan protein.
Tak disangkal kalau kita bisa menyelesaikan masalah ini dengan cepat, tak ada yang bisa dibilang lambat setidaknya untuk kelompok masalah NP.
Pelipatan protein (protein folding) dengan cepat berarti bisa disebut sebagai cara penyembuhan kanker dengan cepat pula. Kita berarti sudah tidak perlu takut kanker kalau kita sudah menemukan mesin yang bisa melakukan pelipatan protein dengan cepat dan tepat.
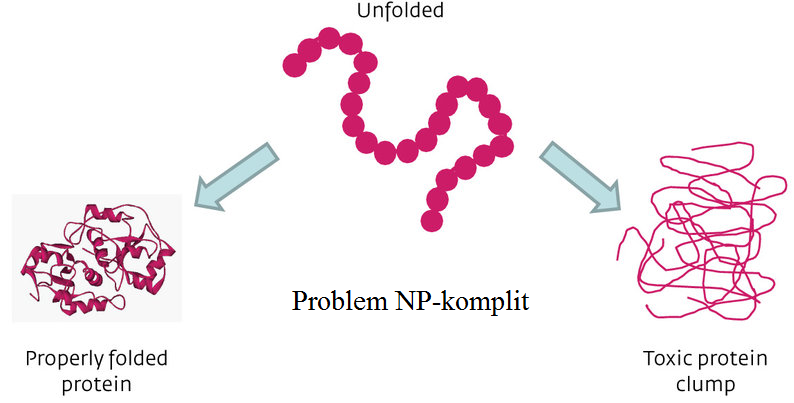
Apabila ditemukan mesin yang bisa menyelesaikan masalah NP-komplit dengan cepat, maka kita akan dengan cepat dan mudah membuat protein penyembuh kanker, begitu juga dengan efeknya yang bisa saja bersifat toksik atau menyembuhkan.
Tapi bagaimana kita bisa membuat mesin semacam itu?
Kita bisa memulai dari membuat mesin penyelesaian Sudoku yang sangat cepat. Sudoku adalah masalah NP-komplit. Jika kita bisa membuat suatu mesin yang bisa menyelesaikan Sudoku dengan cepat dan tepat berarti kita bisa meluruhkan seluruh NP menjadi P.
Selain Sudoku bisa kita mulai dari permainan lain seperti Battleship, Freecell, Mastermind, Tetris, Pembuatan Teka-Teki Silang, Minesweeper, bahkan permainan klasik seperti Super Mario Brother dan Metroid!
Jika kita bisa menemukan satu mesin yang benar-benar cepat untuk menyelesaikan satu saja game diatas dengan cepat dan tepat, maka itu bisa diaplikasikan ke kehidupan normal untuk melipat protein untuk penyembuhan kanker, untuk kegiatan ekonomi, dan sebagainya dalam NP!
Jadi ya, semua intinya adalah penyederhanaan sebuah penyelesaian.
Apa sesederhana mungkin itu bisa? Belum tentu, opini publik dari ilmuwan kompleksivitas menunjukkan bahwa sekitar 83% menyatakan P≠NP dan 9% menyatakan P=NP, sedangkan sisanya berpendapat lain atau abstain. Ini menunjukkan kemungkinan mendapatkan mesin impian semacam itu akan menempuh jalan sulit atau mungkin tidak ada sama sekali!
Namun tidak ada yang akan menyangka pernyataan P=NP akan menyebabkan implikasi yang mendalam. Karena orang tidak akan bisa menentukan dan mengapresiasi atas sebuah kerja keras dan kejeniusan, setuju? Karena orang sudah tidak mementingkan apa yang menjadi proses, melainkan jawaban yang tepat dan cepat.
Pernyataan terakhir dibawah ini bisa jadi kenyataan kalau-kalau memang terjadi, P=NP.
Ada beberapa masalah yang perlu kita ketahui dengan cepat namun masalahnya berbasis NP. Seperti optimalisasi pasar, optimalisasi tingkat kepuasan, menentukan jadwal bekerja yang optimal dengan maksimal, menentukan rute jalan terbaik dengan cepat dan bahkan pelipatan protein.
Tak disangkal kalau kita bisa menyelesaikan masalah ini dengan cepat, tak ada yang bisa dibilang lambat setidaknya untuk kelompok masalah NP.
Pelipatan protein (protein folding) dengan cepat berarti bisa disebut sebagai cara penyembuhan kanker dengan cepat pula. Kita berarti sudah tidak perlu takut kanker kalau kita sudah menemukan mesin yang bisa melakukan pelipatan protein dengan cepat dan tepat.
Quote:

Apabila ditemukan mesin yang bisa menyelesaikan masalah NP-komplit dengan cepat, maka kita akan dengan cepat dan mudah membuat protein penyembuh kanker, begitu juga dengan efeknya yang bisa saja bersifat toksik atau menyembuhkan.
Tapi bagaimana kita bisa membuat mesin semacam itu?
Kita bisa memulai dari membuat mesin penyelesaian Sudoku yang sangat cepat. Sudoku adalah masalah NP-komplit. Jika kita bisa membuat suatu mesin yang bisa menyelesaikan Sudoku dengan cepat dan tepat berarti kita bisa meluruhkan seluruh NP menjadi P.
Selain Sudoku bisa kita mulai dari permainan lain seperti Battleship, Freecell, Mastermind, Tetris, Pembuatan Teka-Teki Silang, Minesweeper, bahkan permainan klasik seperti Super Mario Brother dan Metroid!
Jika kita bisa menemukan satu mesin yang benar-benar cepat untuk menyelesaikan satu saja game diatas dengan cepat dan tepat, maka itu bisa diaplikasikan ke kehidupan normal untuk melipat protein untuk penyembuhan kanker, untuk kegiatan ekonomi, dan sebagainya dalam NP!
Jadi ya, semua intinya adalah penyederhanaan sebuah penyelesaian.
Apa sesederhana mungkin itu bisa? Belum tentu, opini publik dari ilmuwan kompleksivitas menunjukkan bahwa sekitar 83% menyatakan P≠NP dan 9% menyatakan P=NP, sedangkan sisanya berpendapat lain atau abstain. Ini menunjukkan kemungkinan mendapatkan mesin impian semacam itu akan menempuh jalan sulit atau mungkin tidak ada sama sekali!
Namun tidak ada yang akan menyangka pernyataan P=NP akan menyebabkan implikasi yang mendalam. Karena orang tidak akan bisa menentukan dan mengapresiasi atas sebuah kerja keras dan kejeniusan, setuju? Karena orang sudah tidak mementingkan apa yang menjadi proses, melainkan jawaban yang tepat dan cepat.
Pernyataan terakhir dibawah ini bisa jadi kenyataan kalau-kalau memang terjadi, P=NP.
Quote:
“Jika P=NP, maka dunia akan terlihat berbeda dari apa yang telah kita asumsikan sebelumnya. Tidak ada nilai spesial dalam ‘kreativitas’, tidak ada perbedaan yang mendasar dari menyelesaikan masalah dengan mengenali jawaban. Kalau pun ada seseorang yang dapat mengapresiasi sebuah simfoni adalah Mozart, dan kalau pun juga ada seseorang yang dapat mengikuti sebuah argumen tahap demi tahap hanyalah Gauss.” Scott Aaronson.
Sekian gan bagi-bagi ilmunya, gak nolak:
 dan silahkan di
dan silahkan di  dan silahkan juga dikomen
dan silahkan juga dikomenSumber: P vs. NP Computational Complexity Zoo, Wikipedia
Sumber Gambar: Google, Wikipedia
Trit Ane Yang Lain:
Dunia dengan 10 Dimensi, Sebuah Pandangan Baru untuk Menggambarkan Alam Semesta (Hot Thread)
4 Gaya Fundamental yang Membentuk Alam Semesta (Top Thread)
Materi dan Anti-Materi, Sebuah Simetri yang Hilang
Mengenal Heat Death, Skenario Akhir Alam Semesta
Diubah oleh Qidran 26-11-2017 00:50
tien212700 memberi reputasi
1
4.5K
Kutip
14
Balasan
Komentar yang asik ya
Urutan
Terbaru
Terlama
Komentar yang asik ya
Komunitas Pilihan