- Beranda
- Komunitas
- News
- Sains & Teknologi
Euler Identity
TS
paraparadox
Euler Identity
WARNING, KALKULUS ALERT
Ini adalah tutorial untuk menurunkan rumus euler.
Koreksi diterima, saya bukan anak matematika (cuma hobi), newbie main latex dan bukan orang sombong.
dan gw fanboy euler thx/
Spoiler for gambar:
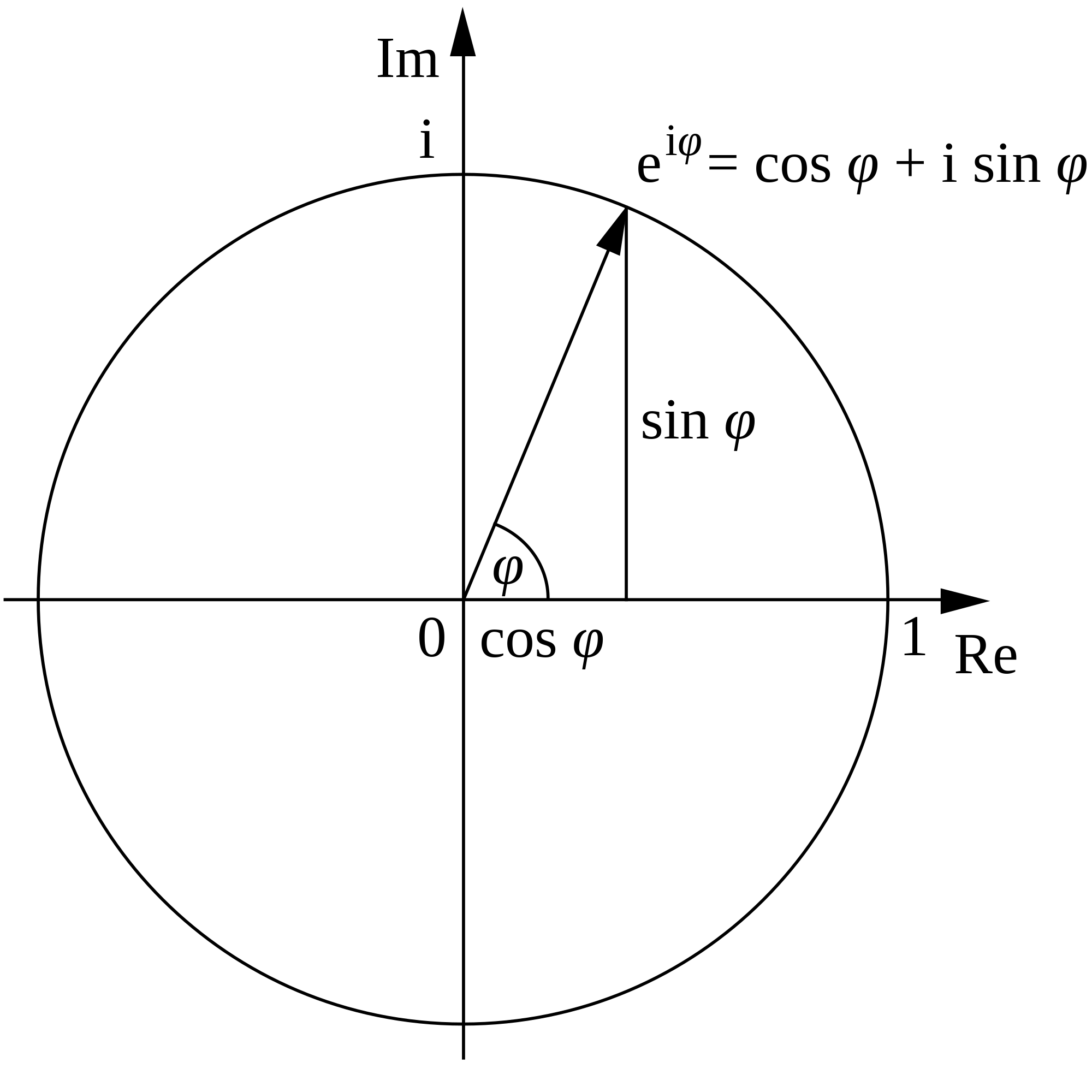
Pertama tama kita mulai dari lingkaran dengan titik pusat 0,0
sumbu x melambangkan bilangan Real, sedangkan sumbu y melambangkan bilangan Imajener
nah kalau belum tahu apa itu bilangan imajener, gampangnya i kuadrat hasilnya adalah minus 1
ada dua cara menulis posisi titik di suatu bidang. bisa pakai kartiseus (x,y) atau pakai sistem polar (r,sudut)
lingkaran tersebut berjari-jari katakanlah r, coba lihat segitiganya, anggaplah titik puncak segitiga yang ada di lingkaran. titik itu kita sebut titik z
anggaplah sudut dari segitiga itu kita sebut \varphi
jadi z bisa kita tulis
(a adalah alas segitiga (yang horizontal), b adalah tingginya(yang vertikal), tapi karena b ada di lingkup imajiner, kita tulis b x i)
dan pakai trigonometri SMA, bisa kita dapat a dan b dari sudut dan jari jari lingkaran, jadi yang horizontal itu r cos \varphi , dan yang vertikal r i sin \varphi
dan kita masukkan ke persamaan terdahulu, maka z akan menjadi
------------------
untuk mudahnya, kita anggap jari jari lingkaran ini satu, r=1 maka
pakai diferensial, turunkan dengan d varphi. turunan cos adalah -sin, turunan sin adalah cos. sedangkan i konstan! jadi gak usah diubah-ubah
keluarkan i, ingat bahwa i adalah akar -1, atau i kuadrat = -1 , maka
perhatikan yang dalam kurung. lihat keatas, yang didalam kurung adalah z, maka kita ganti dengan z
pindahkan z ke kiri, pakai perkalian silang biasa
integralkan kedua ruas
dz/z diintegral dapat ln, d varphi diintegral ya dapat varphi
pangkatkan e dengan kedua ruas, yang belum tahu e, e itu natural logarithm. angkanya sendiri ane lupa

e pangkat lnz adalah z, maka
cantik kan?
------------
masih ingat nilai z?
masukkan ke persamaan
ini identitas euler, bekerja berapapun sudut yang ada. nah kita lihat kalau sudutnya adalah pi, ganti varphi dengan pi
cos pi adalah -1, sin pi adalah 0
sedikit pengaturan, dannnnn
tadaaaa......Quod Erat Demostrandum
Behold mortals, rumus paling cantik yang ada di dunia matematika

Diubah oleh paraparadox 21-11-2015 12:36
0
9.1K
42
Komentar yang asik ya
Urutan
Terbaru
Terlama
Komentar yang asik ya
Komunitas Pilihan